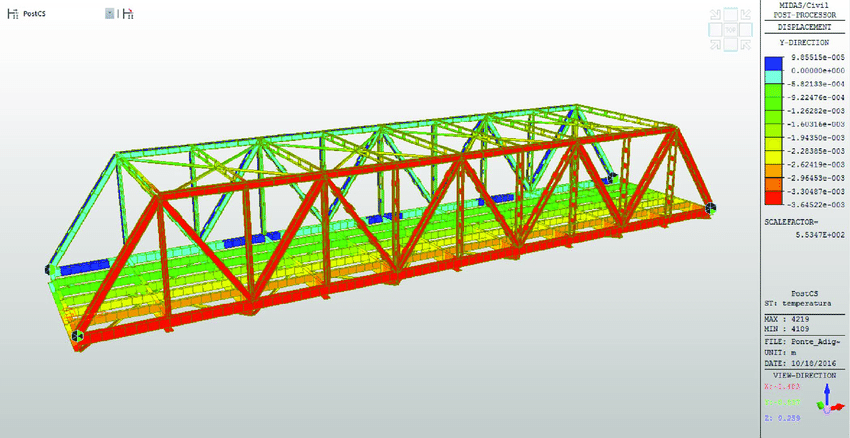
Hitung Stabilitas Crane Barge

Selamat datang di artikel singkat mengenai stabilitas floating crane. Artikel ini bertujuan untuk memperkenalkan teknik verifikasi cepat yang dapat digunakan untuk menentukan stabilitas crane pada tongkang menggunakan prinsip pendulum klasik. Banyak dari kita mungkin pernah mengalami atau belajar tentang pendulum ini selama pelajaran fisika di sekolah menengah, dan sekarang prinsip ini akan diterapkan dalam konteks yang berbeda.
Menentukan stabilitas crane pada tongkang atau kapal, atau struktur lainnya yang mengapung, berkaitan erat dengan menentukan elastisitas atau kekakuan dari sistem secara keseluruhan. Pengenalan kekakuan adalah poin utama dalam penilaian stabilitas ini. Bagaimana cara mengenali kekakuan ini dan bagaimana cara menghitungnya? Artikel ini akan menunjukkan penggunaan prinsip pendulum untuk memberikan pemahaman yang lebih baik tentang apa yang terjadi dan bagaimana teknik pemindaian cepat ini dapat dilakukan dengan perhitungan sederhana.
Pada gambar ilustrasi, terdapat dua pendulum yang digambarkan. Pendulum pertama adalah beban itu sendiri yang tergantung di atas crane, sedangkan pendulum kedua adalah nilai GM, yang merupakan nilai umum dalam fisika maritim. Nilai GM tidak akan dijelaskan dalam artikel ini karena dianggap sebagai informasi dasar yang sudah diketahui banyak orang. Nilai GM adalah semacam pendulum virtual di mana nilai G melambangkan posisi pusat gravitasi (COG) dan nilai M melambangkan titik rotasi dari kombinasi crane-tongkang sebagai poros pivot.

Dua pendulum ini menentukan kekakuan keseluruhan dari situasi. Pada gambar dikiri, beban digambarkan di bawah crane, sementara gambar tengah menunjukkan tongkang yang juga direpresentasikan sebagai pendulum. Ekspresi yang menggambarkan kekakuan rotasi pendulum ditunjukkan di bagian bawah gambar kiri. Rumus ini menyatakan bahwa kekakuan adalah massa di ujung pendulum dikalikan gravitasi dan panjang pendulum. Untuk pendulum GM, rumus ini serupa, yakni massa total atau perpindahan air dari kombinasi vessel-crane dikalikan dengan gravitasi dan panjang pendulum GM.

Penting untuk memahami bahwa ketika beban dipindahkan dari dek keatas, akan ada perubahan signifikan dalam stabilitas sistem. Situasi di mana beban berada di udara hanya berbeda beberapa sentimeter secara visual, namun ini menciptakan perbedaan besar dalam stabilitas secara matematis. Posisi pusat gravitasi harus diperhitungkan di puncak crane, yang berarti kekakuan (stiffeness) sistem akan berkurang secara signifikan. Pemeriksaan standar terhadap tinggi metacentric (GM) pada tongkang saat mempersiapkan pengangkatan dengan carne maka nilai GM dapat dihitung menggunakan rumus berikut:
GM = BM + KB – KG
di mana:
- GM = metacenter ke pusat gravitasi,
- KB = lunas ke pusat buoyancy,
- KG = lunas ke pusat gravitasi (COG),
- BM = metacenter ke pusat buoyancy.
Dalam situasi di mana crane tidak membawa beban, stabilitas dapat diuji dengan mengurangi massa dari tongkang atau kapal. Dengan mengurangi massa, stabilitas akan berkurang setiap saat. Ada titik di mana sistem menjadi tidak stabil secara keseluruhan jika massa berkurang terlalu banyak. Saat crane membawa beban, pusat gravitasi sistem akan bergeser ke puncak crane. Hal ini sangat mempengaruhi stabilitas karena massa di dek berkurang dan massa di atas crane bertambah. Stabilitas berkurang secara signifikan saat beban diangkat dari dek dan mencapai suatu ketinggian tertentu saat lifting.

Selain itu, dinamika lain seperti pengaruh angin atau gerakan kapal dapat menyebabkan beban bergerak ke samping atau ke atas relatif terhadap boom. Pergeseran ini menambahkan momen tambahan yang dapat menyebabkan destabilisasi sistem. Oleh karena itu, memahami faktor-faktor yang mempengaruhi kestabilan melalui prinsip pendulum ini sangat penting.

Teknik perhitungan cepat ini menggunakan dua prinsip pendulum yang telah dijelaskan diatas, yaitu garis beban dan nilai GM. Stiffness dari kedua pendulum ini dapat dihitung dan dibandingkan untuk memberikan gambaran kasar tentang stabilitas sistem. Sebagai contoh, jika faktor amplifikasi sebesar 1,64, ini berarti sudut guling satu derajat akan menghasilkan kemiringan tongkang sebesar 1,64 derajat. Situasi ini dianggap rapuh dan harus dievaluasi lebih lanjut untuk memastikan keamanan operasi.
Sebagai kesimpulan, meskipun teknik hitung cepat ini memberikan gambaran awal tentang kestabilan, perhitungan yang lebih mendetail tetap dibutuhkan. Penggunaan rating yang telah dihitung sebelumnya sangat penting untuk memastikan keamanan dalam operasi pengangkatan. Rating mengintegrasikan berbagai faktor seperti tinggi metacentric dan kekakuan sistem. Teknik pemindaian cepat ini bermanfaat ketika waktu terbatas, namun untuk operasi yang aman, selalu diperlukan perhitungan yang lebih rinci.
Semoga artikel ini memberikan wawasan yang berguna dan meningkatkan pemahaman tentang pentingnya stabilitas dalam operasi pengangkatan di lingkungan maritim.