Sea Transport Loads - Tongkang

Read Time:9 Minute, 25 Second

Tulisan ini membahas analisis beban yang bekerja pada struktur jacket selama transportasi laut menggunakan tongkang. Analisis mencakup efek translasi dan efek angular dari gerakan tongkang yang meliputi rolling, pitching, dan heaving. Persamaan matematis dan perhitungan akselerasi dikembangkan berdasarkan prinsip dinamika dan gerak harmonik sederhana untuk memastikan integritas struktur selama transportasi.

Kata kunci: Transportasi laut, struktur jacket, akselerasi, rolling, pitching, heaving

1. PENDAHULUAN

Transportasi struktur jacket lepas pantai melalui laut merupakan tahap kritis yang memerlukan analisis beban yang cermat. Struktur jacket yang ditransportasikan menggunakan tongkang akan mengalami berbagai gerakan dinamis akibat kondisi laut. Gerakan-gerakan ini menghasilkan beban tambahan yang harus diperhitungkan dalam desain sistem transportasi.

1.1 Latar Belakang

Selama transportasi laut, jacket tidak hanya mengalami beban statis dari berat sendiri, tetapi juga beban dinamis akibat gerakan tongkang. Gerakan tongkang yang signifikan meliputi:

Rolling (φ): Gerakan menggulung pada sumbu longitudinal
Pitching (θ): Gerakan mengangguk pada sumbu transversal
Heaving: Gerakan vertikal naik-turun

Gerakan lain seperti sway, surge, dan yaw diabaikan dalam analisis transportasi laut karena kontribusinya yang relatif kecil terhadap beban struktur.

1.2 Parameter Desain

Berdasarkan Specification for Offshore Installation section 5.2.2 Transportation Engineering, parameter gerakan tongkang yang digunakan adalah:

Parameter	Amplitudo	Periode (T)
Roll (φ)	±20.0°	10.0 detik
Pitch (θ)	±10.0°	10.0 detik
Heave	0.2 g	–

2. METODOLOGI ANALISIS

Analisis beban transportasi laut terbagi dalam dua komponen utama:

Efek Translasi: Akibat inklinasi tongkang
Efek Angular: Akibat percepatan angular dan sentripetal

3. EFEK TRANSLASI

3.1 Dasar Teori

Ketika tongkang mengalami inklinasi akibat rolling atau pitching, massa struktur yang berada di atas tongkang akan mengalami perpindahan komponen gaya. Gaya berat (W = mg) yang awalnya vertikal akan terdekomposisi menjadi komponen sejajar dan tegak lurus terhadap permukaan tongkang yang miring.

3.2 Ilustrasi Efek Translasi

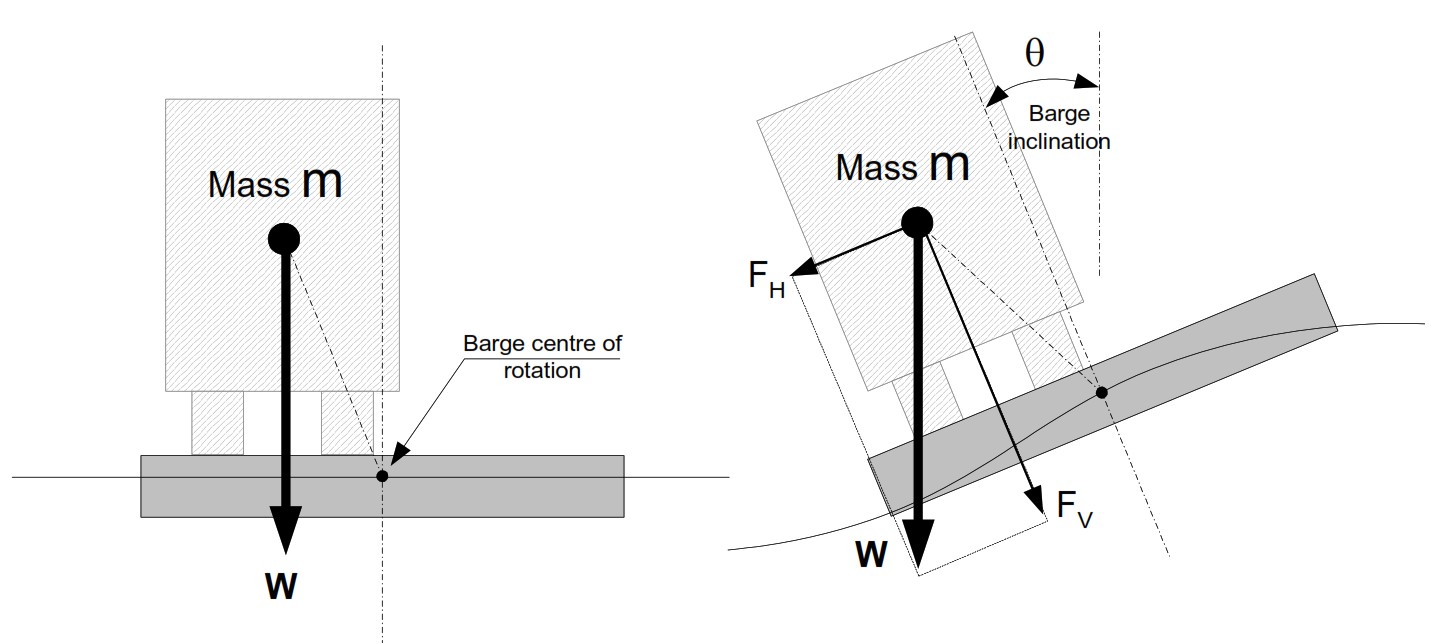
Komponen gaya:
F_H = W sin(α) + m·a_heave → (Horizontal)
F_V = W cos(α) → (Vertikal)

3.3 Persamaan Dasar

Komponen gaya yang bekerja pada massa m akibat inklinasi tongkang adalah:

Komponen Horizontal:

$\boxed{F_H=W\cdot sin(\alpha)+m \cdot a_{heave}=m\cdot g\cdot sin(\alpha)+m \cdot a_{heave}}$

Komponen Vertikal:

$\boxed{F_V=W\cdot cos(\alpha) = m\cdot g\cdot cos(\alpha)}$

Dimana:

W = Berat massa (N)
m = Massa (kg)
g = Percepatan gravitasi (9.81 m/s²)
α = Sudut inklinasi (φ untuk roll, θ untuk pitch)
a_heave = Percepatan heave (0.2g)

3.4 Akselerasi Translasi

Akselerasi yang dialami massa dapat dinyatakan sebagai:

Akselerasi Horizontal:

$\boxed{a_h=\frac{m}{F_H}=g\cdot sin(\alpha)\pm a_{heave}}$

Akselerasi Vertikal:

$\boxed{a_h=\frac{m}{F_H}=g\cdot sin(\alpha)\pm a_{heave}}$

Tanda ± pada heave menunjukkan kondisi heave positif (naik) atau negatif (turun).

3.5 Perhitungan Akselerasi untuk Berbagai Kasus

Kasus 1: Roll + Heave (φ = +20°, heave = +0.2g)

$a_h=g\cdot sin(20°)+0.2g=9.81×0.342+0.2×9.81=3.355+1.962=5.317 m/s^2$

$a_v=g\cdot cos(20°)+0.2g=9.81×0.940+1.962=9.221+1.962=11.183 m/s^2$

$a_v=1.140g\approx 1.128g$

Kasus 2: Roll – Heave (φ = +20°, heave = -0.2g)

$a_h=g\cdot sin(20°)−0.2g=0.342g−0.2g=0.142g\approx 0.274g$

$a_v=g\cdot cos(20°)−0.2g=0.940g−0.2g=0.740g\approx 0.248g$

Kasus 5: Pitch + Heave (θ = +10°, heave = +0.2g)

$a_h=g\cdot sin(10°)+0.2g=9.81×0.174+1.962=1.707+1.962=3.669 m/s^2$

$a_h=0.374g\approx 0.208g$

$a_v=g\cdot cos(10°)+0.2g=9.81×0.985+1.962=9.663+1.962=11.625 m/s^2$

$a_v=1.185g\approx 1.182g$

Kasus Kombinasi: 80% Roll + 60% Pitch + Heave

Untuk kombinasi rolling dan pitching dengan faktor reduksi:

$a_\text{h,roll}=g\cdot sin(0.8×20°)=g\cdot sin(16°)=0.276g\approx 0.121g$

$a_\text{h,pitch}=g\cdot sin(0.6×10°)=g\cdot sin(6°)=0.105g\approx 0.208g$

Akselerasi horizontal total:

$a_h=\sqrt{a^2_\text{h,roll}+a^2_\text{h,pitch}}+0.2g=\sqrt{(0.121)^2+(0.208)^2}+0.2g$

$a_h=\sqrt{0.0146+0.0432}+0.2g=0.240g+0.2g=0.329g$

Akselerasi vertikal:

$a_v=\sqrt{cos^2(16°)\cdot cos^2(6°)}+0.2g=1.148g$

3.6 Ringkasan Faktor Akselerasi Translasi

Kasus	Kondisi	a_h (g)	a_v (g)
1	Roll +20° + Heave	0.410	1.128
2	Roll +20° – Heave	0.274	0.248
3	Roll -20° + Heave	0.410	1.128
4	Roll -20° – Heave	0.274	0.248
5	Pitch +10° + Heave	0.208	1.182
6	Pitch +10° – Heave	0.139	0.212
9-12	80% Roll + 60% Pitch + Heave	0.329	1.148
13-16	80% Roll + 60% Pitch – Heave	0.219	0.235
17-20	60% Roll + 80% Pitch + Heave	0.247	1.163
21-24	60% Roll + 80% Pitch – Heave	0.165	0.225

4. EFEK ANGULAR

4.1 Dasar Teori Gerak Harmonik

Gerakan rolling dan pitching tongkang mengikuti prinsip gerak harmonik sederhana (Simple Harmonic Motion). Persamaan umum gerak harmonik untuk sudut adalah:

$\boxed{a_h=\frac{m}{F_H}=g\cdot sin(\alpha)\pm a_{heave}}$

Dimana:

θ(t) = Sudut pada waktu t (radian)
θ_MAX = Amplitudo maksimum (radian)
ω = Frekuensi angular (rad/s)
t = Waktu (detik)

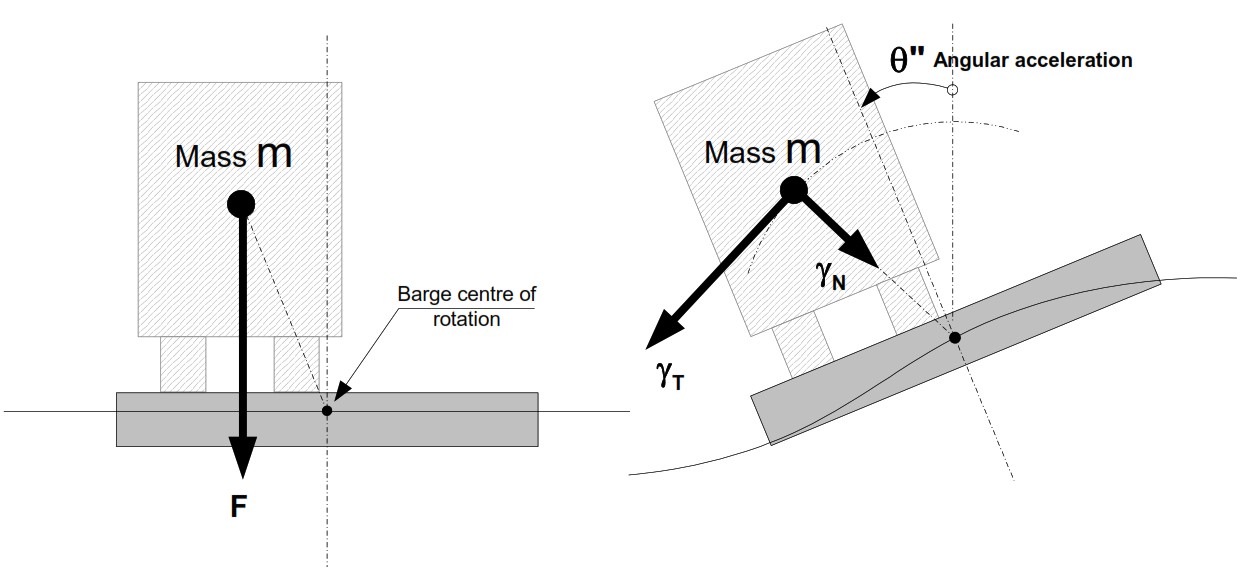
4.2 Ilustrasi Efek Angular

4.3 Kecepatan dan Percepatan Angular

Kecepatan Angular:

$\boxed{\omega=\frac{d\theta}{dt}=\theta_{MAX}\cdot \omega cos(\omega t)}$

Percepatan Angular:

$\boxed{\alpha=\frac{d^2\theta}{dt}=-\theta_{MAX}\cdot \omega^2 cos(\omega t)}$

Percepatan Angular Maksimum:

$\boxed{\alpha_\text{MAX}=\theta_\text{MAX}\cdot \omega^2=\theta_\text{MAX}\left( \frac{2\pi}{T} \right)^2}$

4.4 Perhitungan Percepatan Angular

Untuk Rolling (φ = 20°)

Konversi ke radian:

$\omega_\text{MAX}=20°×180°\pi=0.349 \text{ radian}$

Frekuensi angular:

$\omega_\text{MAX}=20°\frac{\pi}{180°}\pi=0.349 \text{ radian}$

Percepatan angular maksimum:

$\alpha_\text{roll}=\omega_\text{MAX}\cdot \omega^2=0.349×(0.628)^2=0.349×0.395=0.138 \text{ rad}/s^2$

Konversi ke derajat:

$α_\text{roll}=0.138×\frac{180°}{\pi}=7.895 \text{ deg}/s^2$

Untuk Pitching (θ = 10°)

Konversi ke radian:

$\theta_\text{MAX}=10°×\frac{180°}{\pi}=0.175 \text{ radian}$

Percepatan angular maksimum:

$α_\text{pitch}=\theta_\text{MAX}\cdot \omega^2=0.175×(0.628)^2=0.175×0.395=0.069 \text{ rad}/s^2$

Konversi ke derajat:

$α_\text{pitch}=0.069×\frac{180°}{\pi}=3.947 \text{ deg}/s^2$

4.5 Percepatan Tangensial dan Sentripetal

Percepatan Tangensial:

$\boxed{a_T=R\cdot \alpha}$

Dimana R adalah jarak dari pusat rotasi tongkang ke lokasi massa.

Percepatan Sentripetal:

$\boxed{a_N=R\cdot \omega^2=R\left( \frac{d\theta}{dt} \right)^2}$

Catatan Penting: Dalam analisis transportasi laut, efek percepatan sentripetal diabaikan karena nilai kecepatan angular yang relatif kecil membuat kontribusinya tidak signifikan dibandingkan dengan percepatan tangensial.

4.6 Kombinasi Gaya

Gaya total yang bekerja pada setiap massa struktur adalah kombinasi dari:

Gaya gravitasi (berat sendiri)
Gaya akibat percepatan translasi (horizontal dan vertikal)
Gaya akibat percepatan tangensial (rolling atau pitching)

Modul TOW melakukan perhitungan untuk setiap massa struktur dengan menghitung gaya tangensial dari rolling atau pitching, kemudian mengombinasikannya dengan beban gravitasi.

5. APLIKASI DALAM ANALISIS STRUKTUR

5.1 Metodologi Analisis

Analisis transportasi laut struktur jacket menggunakan pendekatan berikut:

Identifikasi Massa: Setiap komponen struktur diidentifikasi dengan massa dan lokasinya relatif terhadap pusat rotasi tongkang
Perhitungan Akselerasi: Untuk setiap kasus beban, akselerasi translasi dan angular dihitung
Kombinasi Beban: Beban dinamis dikombinasikan dengan beban statis (berat sendiri dan beban angin)
Analisis Struktural: Analisis tegangan dan defleksi dilakukan untuk memastikan struktur aman

5.2 Kasus Beban Kritis

Dari 24 kasus beban yang dianalisis, kasus-kasus berikut umumnya menghasilkan beban maksimum:

Kasus 1 dan 3: Roll maksimum dengan heave positif menghasilkan akselerasi vertikal terbesar (1.128g)
Kasus 9-12: Kombinasi 80% roll dan 60% pitch dengan heave positif menghasilkan akselerasi horizontal maksimum (0.329g)
Kasus 17-20: Kombinasi 60% roll dan 80% pitch dengan heave positif menghasilkan kondisi beban seimbang

5.3 Kriteria Desain

Sistem seafastening dan struktur jacket harus dirancang untuk menahan:

Akselerasi horizontal maksimum: 0.410g (dari kasus roll murni)
Akselerasi vertikal maksimum: 1.182g (dari kasus pitch + heave)
Akselerasi angular: 7.895 deg/s² (roll) dan 3.947 deg/s² (pitch)

6. KESIMPULAN

Analisis beban transportasi laut pada struktur jacket memerlukan pertimbangan efek translasi dan efek angular dari gerakan tongkang
Efek translasi menghasilkan akselerasi horizontal hingga 0.410g dan akselerasi vertikal hingga 1.182g
Efek angular menghasilkan percepatan angular 7.895 deg/s² untuk rolling dan 3.947 deg/s² untuk pitching
Kombinasi gerakan rolling, pitching, dan heaving menghasilkan 24 kasus beban yang harus dianalisis untuk memastikan keamanan struktur
Percepatan sentripetal diabaikan dalam analisis karena nilainya yang tidak signifikan
Metodologi ini sesuai dengan Specification for Offshore Installation section 5.2.2 Transportation Engineering

7. REFERENSI

API RP 2A-WSD (2014), “Recommended Practice for Planning, Designing and Constructing Fixed Offshore Platforms – Working Stress Design”, American Petroleum Institute, Washington D.C.
Noble Denton (2013), “Guidelines for Marine Transportations”, Noble Denton Group Limited, London, UK.
DNV-GL (2015), “Offshore Standard DNV-OS-H101: Marine Operations, General”, Det Norske Veritas – Germanischer Lloyd, Norway.
GL Noble Denton 0027/ND (2010), “Specification for Offshore Installation”, Guidelines for Marine Operations, Rev 4.
Chakrabarti, S.K. (2005), “Handbook of Offshore Engineering”, Elsevier Ocean Engineering Series, Volume 1, Amsterdam.
Dawson, T.H. (1983), “Offshore Structural Engineering”, Prentice-Hall Inc., New Jersey.
McCormick, M.E. (2010), “Ocean Engineering Mechanics: With Applications”, Cambridge University Press, UK.
Gerwick, B.C. (2007), “Construction of Marine and Offshore Structures”, CRC Press, Third Edition, Boca Raton, Florida.
ISO 19901-6 (2009), “Petroleum and natural gas industries – Specific requirements for offshore structures – Part 6: Marine operations”, International Organization for Standardization.
Wilson, J.F. (2003), “Dynamics of Offshore Structures”, John Wiley & Sons Inc., Second Edition, New Jersey.

LAMPIRAN A: NOTASI DAN SIMBOL

Simbol	Deskripsi	Satuan
φ	Sudut roll	° atau radian
θ	Sudut pitch	° atau radian
α	Sudut inklinasi umum	° atau radian
ω	Frekuensi angular	rad/s
α” atau α	Percepatan angular	rad/s² atau deg/s²
T	Periode osilasi	detik
g	Percepatan gravitasi	m/s²
m	Massa	kg
W	Berat (= mg)	N
R	Jarak dari pusat rotasi	m
a_h	Akselerasi horizontal	m/s² atau g
a_v	Akselerasi vertikal	m/s² atau g
a_T	Akselerasi tangensial	m/s²
a_N	Akselerasi sentripetal	m/s²
F_H	Gaya horizontal	N
F_V	Gaya vertikal	N

Catatan: Tulisan ini disusun berdasarkan dokumen teknis “Acceleration Calculations Theory” untuk analisis transportasi laut struktur jacket lepas pantai. Perhitungan dan metodologi mengikuti standar internasional untuk operasi marine dalam industri minyak dan gas.

Disusun untuk keperluan dokumentasi teknis transportasi struktur offshore

About Post Author

Muh. Burhanuddin

Industrial Engineer, Specialist in Heavy Cargo Transportation and Heavy Lifting Works. Hobby in computer programming, reading and writing. No occupation except waiting for a prayer time. Ready for working as a surveyor, transport planer, or as lifting engineer.

https://www.alvinburhani.net

Happy

0 %

Sad

0 %

Excited

100 %

Sleepy

0 %

Angry

0 %

Surprise

0 %

About The Author

Muh. Burhanuddin

See author's posts

Sea Transport Loads – Tongkang

1. PENDAHULUAN

1.1 Latar Belakang

1.2 Parameter Desain

2. METODOLOGI ANALISIS

3. EFEK TRANSLASI

3.1 Dasar Teori

3.2 Ilustrasi Efek Translasi

3.3 Persamaan Dasar

3.4 Akselerasi Translasi

3.5 Perhitungan Akselerasi untuk Berbagai Kasus

Kasus 1: Roll + Heave (φ = +20°, heave = +0.2g)

Kasus 2: Roll – Heave (φ = +20°, heave = -0.2g)

Kasus 5: Pitch + Heave (θ = +10°, heave = +0.2g)

Kasus Kombinasi: 80% Roll + 60% Pitch + Heave

3.6 Ringkasan Faktor Akselerasi Translasi

4. EFEK ANGULAR

4.1 Dasar Teori Gerak Harmonik

4.2 Ilustrasi Efek Angular

4.3 Kecepatan dan Percepatan Angular