Menemukan Pusat Gravitasi (CoG)

Ditakuti oleh banyak orang, dipahami oleh sedikit orang, center of gravity (CoG) adalah properti tunggal yang paling diremehkan dan kurang dihargai dari sebuah beban. Karena sebagian besar operasi transport dan lifting melibatkan beban dengan CoG yang cukup terpusat, tidak banyak insentif untuk mendalami teori tentang sesuatu yang tidak dapat dilihat atau diukur dengan meteran.
Namun, jika CoG tidak terpusat, atau beban mendekati batas kemampuan peralatan transport atau lift, maka properti ini menjadi semakin penting yang dapat menentukan keberhasilan atau kegagalan sebuah proyek.
Apa itu Center of Gravity?
Dalam istilah matematis, “Center of gravity adalah titik di mana seluruh massa objek dapat diasumsikan berada”. Ini mungkin terdengar agak abstrak tetapi dengan contoh-contoh di bawah ini akan menjadi jelas. CoG tidak ditentukan oleh bentuk atau ukuran, hanya oleh berat dan lokasi (koordinat) dari setiap komponen individualnya.

Oleh karenanya, jelas bahwa center of gravity dari sebuah kotak persegi berada tepat di tengah kotak tersebut dan bahwa menangani, mengangkat, jacking atau men-transport-nya bukanlah latihan yang rumit dari sudut pandang matematis. Hal ini berubah ketika berhadapan dengan objek yang dibangun dari banyak item individual. Cepat atau lambat, semua orang akan menghadapi situasi ini, di mana hal ini menjadi jauh lebih menantang. Objek-objek tersebut dapat berupa skid yang berisi komponen dari berbagai pemasok atau, misalnya, vessel dengan diameter yang bervariasi, oiler dengan pressure vessel yang terletak di satu sisi atau hanya peti kayu dengan isi yang tidak diketahui dan tanda CoG yang dicat tangan yang mungkin dapat atau tidak dapat percayai.
Industri heavy lifting dan specialized transport menghadapi tantangan kompleks dalam menangani beban dengan karakteristik geometri dan distribusi massa yang bervariasi. Center of Gravity (CoG) adalah titik teoritis dimana seluruh massa objek dapat diasumsikan terkonsentrasi (Van Daal, 2013). Parameter ini menjadi faktor penentu dalam perencanaan rigging, pemilihan equipment, dan eksekusi operasi lifting maupun transport.

Mayoritas operasi melibatkan beban dengan CoG yang relatif terpusat, sehingga mengurangi insentif untuk melakukan analisis mendalam. Namun, ketika CoG tidak terpusat atau beban mendekati kapasitas limit equipment, maka penentuan CoG yang akurat menjadi krusial untuk keselamatan dan keberhasilan operasi (International Cranes and Specialized Transport, 2013).
Rumusan Masalah
Bagaimana menentukan CoG pada objek dengan geometri kompleks dan distribusi massa tidak uniform? Bagaimana mengaplikasikan metode analisis CoG tanpa informasi lengkap tentang berat atau material objek? dan bagaimana dampak ketidakakuratan perhitungan CoG terhadap operasi lifting dan transport?
Disini akan dijelasakan bagaimana mengembangkan metodologi sistematis untuk penentuan CoG pada objek kompleks, memvalidasi metode simplifikasi menggunakan rasio area/volume terhadap massa, dan menganalisis implikasi praktis dari perhitungan CoG dalam operasi lapangan atau field operation.
Harapannya tulisan ini memberikan kontribusi praktis bagi praktisi heavy lifting dan transport engineering dalam meningkatkan akurasi perencanaan rigging, mengurangi risiko operational failure, mengoptimalkan pemilihan dan konfigurasi equipment, dan menyediakan framework metodologi yang dapat direplikasi.
TINJAUAN PUSTAKA
Secara matematis, Center of Gravity didefinisikan sebagai “titik dimana seluruh massa objek dapat diasumsikan berada” (Van Daal, 2013). CoG tidak ditentukan oleh bentuk atau ukuran objek, melainkan oleh distribusi massa dan posisi relatif setiap komponen penyusunnya.
Prinsip Dasar Mekanika
Dalam mekanika klasik, CoG berkaitan erat dengan konsep center of mass dan centroid. Untuk objek dengan distribusi densitas uniform, CoG coincide dengan geometric centroid. Namun untuk objek dengan densitas tidak uniform atau geometri kompleks, penentuan CoG memerlukan analisis lebih mendalam.
Aplikasi dalam Heavy Lifting
Dalam industri heavy lifting, pengetahuan tentang CoG mempengaruhi pemilihan lifting point, konfigurasi sling arrangement, perhitungan load distribution, stabilitas selama lifting dan transport, dan pertimbangan safety factor dalam load chart analysis
Metode Penentuan CoG
Berbagai metode dapat digunakan untuk menentukan CoG:
- Metode Eksperimental: Load cell testing, tilt table method
- Metode Analitis: Mathematical calculation, CAD modeling
- Metode Numerik: Finite Element Analysis (FEA)
Tulisan ini fokus pada metode analitis yang applicable untuk field operations.
Menentukan Center of Gravity
Berikut adalah latihan dengan cara sederhana dalam menentukan center of gravity. Metode ini dapat diterapkan pada setiap objek yang CoG-nya perlu ditentukan. Perhatikan Gambar 1, ini adalah objek dua dimensi, misalnya, pelat baja dengan bentuk acak, yang CoG-nya perlu ditentukan. Ini tidak dapat dilakukan dalam satu langkah, tetapi harus dilakukan dalam serangkaian langkah terpisah.
CATATAN: jarak diberikan dalam meter tetapi ini dapat berupa unit ukuran apa pun: kaki, yard, dll. Untuk hasil perhitungan ini tidak membuat perbedaan.
LANGKAH 1
Pilih lokasi sumbu x dan sumbu y. Ini dapat dipilih di lokasi mana pun karena hasilnya akan tetap sama jika sumbu-sumbu ini dipilih di lokasi yang berbeda.
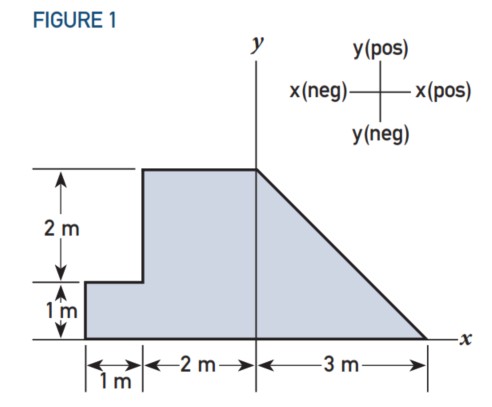
Untuk contoh pada Gambar 1 ini, sumbu x dipilih di dasar objek dan sumbu y dipilih sehingga berjalan lurus ke bawah di antara bentuk segitiga dan persegi panjang.
LANGKAH 2
Pilih sisi mana dari sumbu x yang merupakan sisi positif dan mana yang negatif. Ini diperlukan karena jarak 1-meter dari sumbu y bisa berada di kedua sisi dan tanpa penunjukan “+” atau “-” tidak ada cara untuk mengetahui ini dan, menurut definisi, hasil perhitungan akan salah.
LANGKAH 3
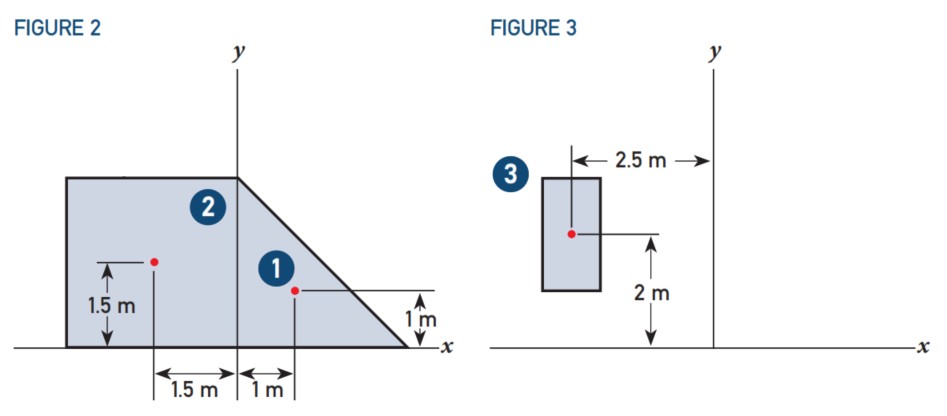
Sekarang objek tersebut dibagi menjadi “sub-objek” yang lebih kecil dan dapat dengan mudah menentukan CoG-nya. Lihat Gambar 2 dan Gambar 3. Tidak ada ilmu di balik pemilihan objek-objek yang lebih kecil ini. Apa pun bisa, selama seluruh objek tercakup, jelas tidak ada yang boleh terlupakan atau tertinggal. Dalam contoh ini telah dipilih:
- Sebuah segitiga (kotak 3 x 3 m dipotong setengah)
- Sebuah kotak (3 x 3 m). Perhatikan bahwa kotak ini termasuk void (rongga kosong)
- Sebuah persegi panjang (1 x 2 m). Ini adalah void dari kotak yang disebutkan di atas pada nomor 2.
LANGKAH 4
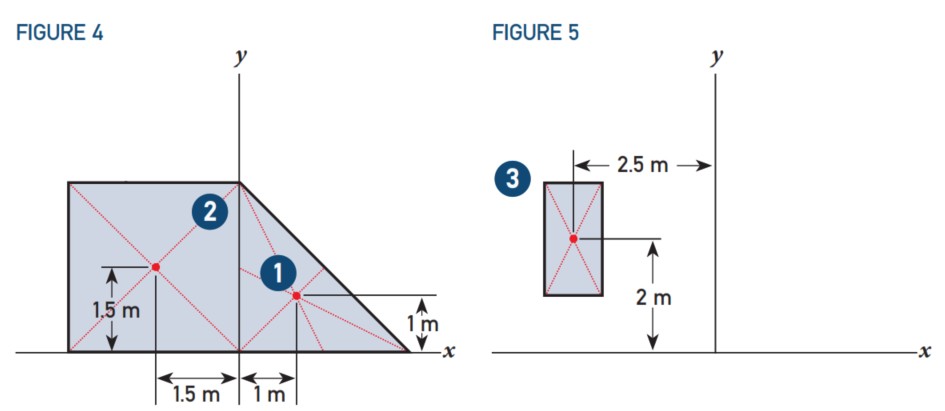
Dari masing-masing sub-objek ini, CoG harus ditentukan dan dinyatakan dalam koordinat. Lihat gambar 4 dan 5. Dengan menggambar garis bantu (dalam warna merah) dari satu sudut ke sudut yang berlawanan, CoG dapat ditemukan untuk kotak dan persegi panjang. Dengan menggambar garis (bantu) dari satu sudut ke tengah sisi yang berlawanan, CoG dapat ditemukan untuk segitiga. CoG ini ditemukan di persimpangan garis-garis bantu ini. Hasilnya adalah sebagai berikut:
- CoG 1. (+1.0, +1.0)
- CoG 2. (-1.5, +1.5)
- CoG 3. (-2.5, +2.0)
LANGKAH 5
Susun Data untuk Perhitungan
| Objek | Koordinat X | Koordinat Y | Berat/Luas |
|---|---|---|---|
| 1 | +1.0 | +1.0 | 4.5 |
| 2 | -1.5 | +1.5 | 9 |
| 3 | -2.5 | +2.0 | -2 (**) |
(**) Karena objek 3 sebenarnya adalah void, berat (luas) perlu dimasukkan sebagai nilai negatif dalam formula.
Formula Perhitungan
Formula untuk menghitung CoG adalah:
CoG = (∑D×W) / ∑W
Dalam kata-kata, lokasi CoG dapat ditemukan dengan menjumlahkan (∑) perkalian jarak dengan berat (luas) dan membaginya dengan penjumlahan semua berat (luas).
LANGKAH 6:
Hitung CoG
Untuk arah x: CoGₓ = [(+1.0×4.5) + (-1.5×9) + (-2.5×-2)] / (4.5+9-2) = -4/11.5 = -0.35
Untuk arah y: CoGᵧ = [(+1.0×4.5) + (+1.5×9) + (+2.0×-2)] / (4.5+9-2) = 13/11.5 = 1.13
CoG dapat ditemukan pada koordinat (-0.35, 1.13)
Hasil Akhir
CoG dapat ditemukan pada koordinat (-0.35, 1.13), lihat gambar 6.
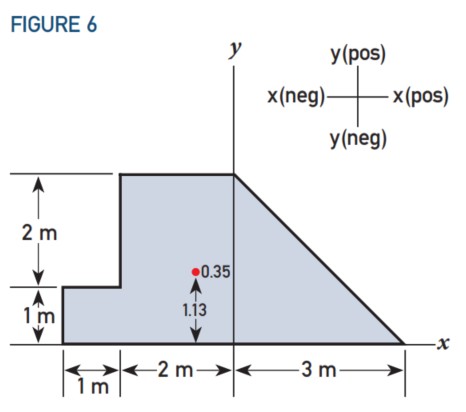
Ketika melakukan perhitungan semacam ini sebaikanya dilakukan secara lebih sering agar khazanah dan pengalaman banyak diperoleh, dan mudah mudahan beberapa langkah di atas dapat digabungkan untuk mempercepat prosesnya. Selamat mencoba!
DAFTAR PUSTAKA
- International Cranes and Specialized Transport. (2013). “Central Focus: The Knowledge on Center of Gravity.” International Cranes and Specialized Transport Magazine, December 2013, pp. 36-37.
- Van Daal, M. (2013). The Art of Heavy Transport. KHL Group Publications. Available at: www.khl.com/books/the-art-of-heavy-transport/
- Beer, F.P., Johnston, E.R., & Eisenberg, E.R. (2010). Vector Mechanics for Engineers: Statics and Dynamics (9th ed.). McGraw-Hill.
- Crane Manufacturers Association of America (CMAA). (2012). CMAA Specification No. 70: Specifications for Top Running Bridge and Gantry Type Multiple Girder Electric Overhead Traveling Cranes.
- Health and Safety Executive (HSE). (2013). Safe Use of Lifting Equipment: Lifting Operations and Lifting Equipment Regulations 1998 (LOLER). HSE Books.
- Sarkar, A. K. (2011). “Center of Gravity Determination of Heavy Engineering Components.” International Journal of Heavy Lifting and Transport, Vol. 8(2), pp. 45-58.